Ancient Mathematics: Quasicrystals in Western and Central Asia
- Caroline Martin

- Dec 16, 2021
- 5 min read
Updated: Dec 18, 2021
Infinite patterns hidden in plain sight in medieval Islamic architecture.
Patterns of repeating geometric shapes are everywhere. Take a quick look around and see if there’s any you can spot - maybe the regular pattern of square ceiling tiles in your classroom, decorative hexagons tiling your kitchen floor, or even a checkerboard pattern decorating your clothes.
When regular geometric shapes fit together and cover a surface, mathematicians call that a tessellation or a tiling. These tilings are everywhere - from the human scale, like the hexagons inside a beehive, all the way down to the atomic scale, like the lattice of atoms that make up solid materials.


Periodic crystal tilings include things like the honeycomb lattice you find inside a beehive or the regular stacks of atoms that make up solid materials
The Art of Tiling
Humans have been using tilings as decoration for thousands of years. Ancient cultures from India to Mesopotamia to the Mediterranean used tiles to create beautiful, complex designs that nonetheless have a simple, repeating pattern to them. When geometric patterns are made from a set number of basic shapes that repeat over and over, they create what’s called a periodic tiling. Periodic tilings have a base unit cell that is moved around and rotated to fill in the space of the plane.
Geometric patterns made from tiles are especially important in Islamic architecture, which avoids using images of people in decoration. Instead, many structures built in the ancient Islamic world were decorated with elaborate geometric designs of repeating squares, circles, stars, or other regular polygons. These decorative patterns are complicated, but they are also highly symmetrical. If you take a section of the pattern, for example, you can translate it (move it up and down or left and right) or rotate it (spin it around) and find other sections that exactly match.

This is an example of a periodic tile pattern. What are the most basic shapes you need to make this pattern? That’s called the unit cell of the crystal. By moving and rotating the unit cell, you can create the repeating pattern of the crystal.


Here are some examples of geometric patterns from an Islamic palace in Spain called the Alhambra. Can you find any repeating elements? What are the base shapes that make up the pattern?
Quasicrystals: An Impossible Pattern?
Humans have been making repeating patterns out of shapes for millennia. But what about a pattern that doesn’t repeat? Is there any way to take some number of shapes and fit them together without a regular, periodic pattern, even if you continue laying down the tiles forever? For a long time, mathematicians thought that this was impossible. It wasn’t until the 1970s and 1980s that modern scientists started seeing evidence for these weird kinds of crystal patterns, called quasiperiodic crystals, or quasicrystals for short. But there’s evidence that humans might have figured out how to create these mysterious, infinite, non-repeating patterns hundreds and hundreds of years ago. This evidence was hidden in plain sight in the geometric tiles of an ancient Islamic building!
But wait, what even is a quasicrystal? For something to be a crystal, it has to fully tile the plane, which means that when you lay down the pieces of your crystal edge-to-edge, it can continue out to infinity with no gaps in between. Quasicrystals can tile the plane, but they aren’t periodic the way that normal crystals are. This means that they don’t have the same translational symmetries that we talked about earlier. In a quasicrystal, you can’t draw a box around a section, move that section over, and continue the pattern. There’s always a mismatch, even if you have a really huge box. You can look out to infinity to try to find a box big enough to repeat the pattern, but you’ll never find it!
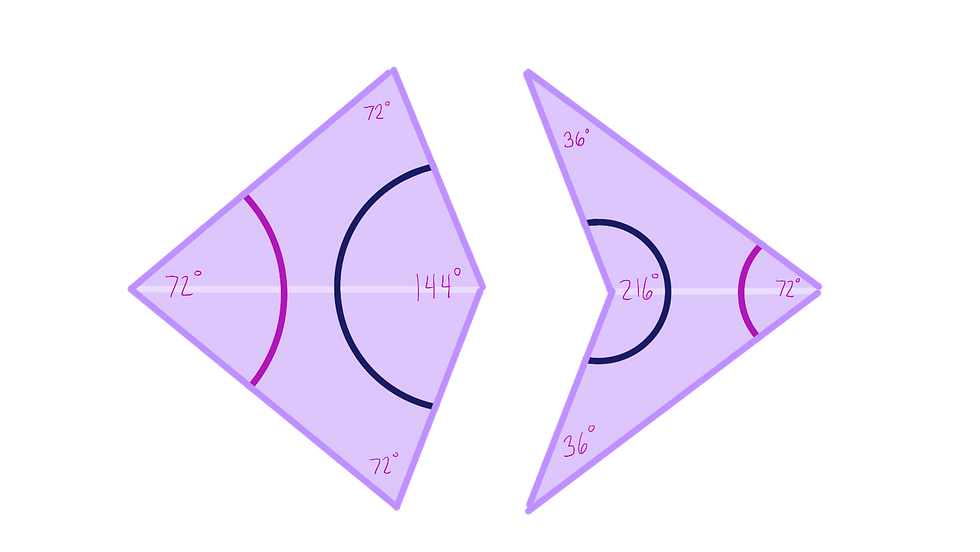
It doesn’t seem like this kind of pattern should be able to exist, but there are actually ways to make a quasicrystal with just a few simple rules. One example is with something called Penrose tiles. With just two simple shapes, called a “kite” and a “dart”, along with some simple rules about how you can connect them, you can create your own quasicrystal pattern (if you’re curious, check out our activities below to learn more about kites and darts and see what you can make).

Can you find a section that matches just by sliding that section left and right? What about by spinning the section around?
Even though the Penrose pattern above wasn’t developed until 1974, we’ve recently found evidence of these kinds of patterns in medieval architecture across Western and Central Asia. Researchers, including physicists and architects, noticed that some ancient buildings, built around 1200 CE, had patterns on them that looked different than the ordered geometric tilings that are typical of the decoration style. On closer inspection, we realized that these ancient tiles were actually patterned the same way as quasicrystals! In some regions, the patterns were almost perfect Penrose tilings, built more than 500 years before Roger Penrose was even born. The few mistakes that do exist in the pattern could easily be fixed by flipping one of the tiles. So scientists think that those flaws are just simple mistakes made by the person arranging the tiles, not mathematical mistakes made by the designers.
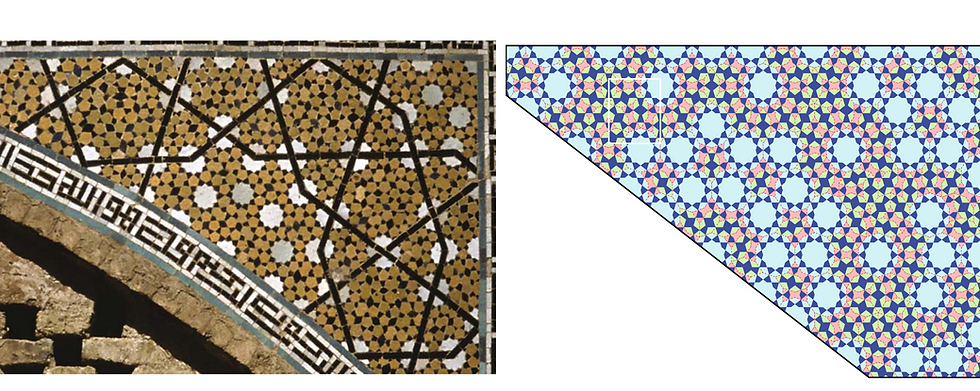
This pattern is found in the Darb-i Imam shrine in Iran, and it was made in 1453. The pattern, recreated from the base shapes (each colored differently), doesn’t have translational symmetry and never repeats, even if you continue it forever.
While these patterns don’t go on forever (or else we’d need an infinite number of tiles and an infinitely long wall!), you could continue the patterns out to infinity using just a few tiles decorated with connected lines, just like the design on the Penrose tiles. These tiles are called girih tiles. They allowed ancient tile artists to make increasingly complicated patterns just by alternating between the tiles they have, like laying down pieces of a puzzle. This process of tessellation is much easier than drawing all the lines with a straightedge and a compass. The final product of zigzagging lines and overlapping geometric shapes is almost dizzying to look at, but there are patterns you can pick up if you look long enough!

The quasicrystal patterns in the Darb-i Imam shrine look very complicated, but are made from just a few repeating tiles.
Hidden in Plain Sight
For centuries, mathematicians and scientists thought that there could be no such thing as a regular pattern that doesn’t repeat. But once Western mathematicians theorized that quasicrystals could exist, evidence of them started turning up everywhere. In rare minerals, in some aluminum alloys, and even in fused sand melted from a nuclear explosion, scientists found nonperiodic crystal structures. The closer that scientists looked, the more examples of quasicrystals they found. But it turns out that humans had already figured out how to make these once-impossible patterns, 500 years ago in Central Asia. We’re just now starting to appreciate the complexity of these patterns in medieval Islamic buildings. What other great discovery could be hidden in plain sight like these ancient quasicrystals? Who knows what you might find if you start looking closely!
Photos courtesy of Wikimedia Commons, "Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture" by P.J. Lu and P.J. Steinhardt, and AlhambraDeGranada.org
Written by Caroline Martin
Edited by Madelyn Leembruggen
Illustrations by Taylor Contreras
Sources and additional readings:
Ancient Islamic architects created perfect quasicrystals by Physics World
Islamic Artisans Constructed Exotic Nonrepeating Pattern 500 Years Before Mathematicians by Scientific American
In Medieval Architecture, Signs of Advanced Math by the New York Times
Make your own tessellations and explore math in ancient cultures!
Define (15 minutes): Identify lines of symmetry. Why are lines of symmetry important for creating periodic tilings?
Play (60-90 minutes): Create a periodic tessellation inspired by M.C. Escher's designs.
Interact (30-45 minutes): Assemble a digital Penrose tiling using kites and darts.
Explore (30-60 minutes): Gather examples of geometry from cultures across the globe.





Comments